题面

给定一个长度为 $5000$ 的正则表达式和一个长度为 $10000$ 的文本串，求文本串最少修改多少次能够被正则表达式识别。

题解

对正则表达式构造 NFA，令 $f(l,i)$ 表达式使用完前 $l$ 个字符后，到达了 NFA 的状态 $i$ 时的最小修改次数，转移方程的形式为求一个 $0/1$ 最短路。

XLex 正则表达式

题面

有一个长度为 $n$ 的未知数组，第 $i$ 个位置的值有有 $k_i$ 种选择，这个位置选择 $V(i,j)$ 的代价 $C(i,j)$。

当你确定数组后，有 $q$ 次询问 $[l, r]$ 区间内的最大值，这个数组的价值就是所有询问的和减去选数时的代价。

数据范围：$1 \le n \le 300, n \le \sum_{i=1}^n k_i \le 3 \cdot 10^5$。

分析

考虑区间 DP，令 $f(l, r)$ 表示确定完区间 $[l, r]$ 的价值。

预处理每个位置 $i$ 被区间 $[l, r]$ 内所有询问覆盖的次数。转移时可以枚举这个区间的某一个位置作为最大值，但是每一个位置有多种选择，这个位置不仅要在价值上比较优，还需要满足比上一层小的限制。

无视上面的区间 DP，我们对于一个点，可以发现这个点产生的贡献关于覆盖次数是一堆一次函数的 $\max$，也就是一个下凸壳。回到上面的 DP，我们在枚举最大值，使用预处理的覆盖次数，可以在凸壳上二分出对应的一次函数，得到最优价值。

其实，我们已经做完了，上面的算法已经能够得到最优解，且最优解一定是合法的。

简单证明一下，我们考虑点 $i$ 和点 $j$，假设点 $i$ 作为大区间时的被覆盖次数为 $x_1$，小区间 $x_2$，点 $j$ 类似地为 $x_3$ 和 $x_4$，显然 $x_1 > x_2, x_3 > x_4$。不妨设两个点 $i < j$ 分别只有两条线段 $f(x) = k_i x - b_i$ 和 $f(x) = k_j x - b_j$，且 $k_i > k_j$。因此，$i$ 必须作为大区间的最大值，而 $j$ 需要在内层。

合法解时的价值为 $k_i x_1 - b_i + k_j x_4 - b_j$，非法解时的价值为 $k_i x_2 - b_i + k_j x_3 - b_j$。

注意到 $x_1 - x_2 = x_3 - x_4$，因为这个差是所有区间左端点在 $i$ 左侧和右端点在 $j$ 右侧。

因此 $k_i (x_1 - x_2) > k_j (x_3 - x_4)$。

B Playlist

给定一个环形的数组 $a_1, a_2, \dots, a_n$，有一个指针 $p$ 在环上进行扫描，如果当前位置和上一个位置的数 $\gcd = 1$，那么删除当前位置，指针移到下一个位置重新开始，直到无法删除。

我们不能暴力模拟，因为每次可能会跳 $O(n)$ 次来找到目标删除的位置。例如：$2 \times 3, 3 \times 5, \dots, p$，每次会删除第一个数。

因此，我们需要优化这个找删除位置的过程。注意到，记 $\text{next}(i)$ 表示在剩下的位置中 $i$ 后面的那一个（环的意义下）。如果 $\gcd(a[i], a[\text{next}(i)]) > 1 $，那么这个 $i$ 位置和他后面的这一对数，在之后永远不会被当作一对删除，因此我们在找删除对的时候，不再需要考虑位置 $i$。因为，我们在不会跳过 $i$ 来删除 $i$ 后面那个，$i$ 后面那个会一直存在，直到 $i$ 被前面的删除，导致其变换前驱。

C Skyline Photo

给定一个排列 $h_1, h_2, \dots, h_n$，将这个数组划分为多个段，每个段的权值是 $h$ 的最小位置 $i$ 的权值 $b_i$，总权值是所有权值的和，求最大权值。

显然，如果权值都是正数那么只要分成长度为 $1$ 的段即可。考虑 $f(i)$ 表示以 $i$ 结尾的最大权值，那么这个权值会一直存活到下一个 $h$ 比它小的位置，这部分维护一个扫描线。然后考虑 $f(i)$ 是怎么得到的，会有两部分转移一部分是从上一个比它小的位置到这个位置的一段区间中取一个最大的，或者是从扫描线中取一个最大的。

D Useful Edges

给定一个带边权的无向图和 $q$ 组条件三元组 $(u,v,l)$。对于边 $(a,b)$，如果存在三元组 $(u,v,l)$ 和一条 $u \to v$ 的路径，满足这条路径权值和小于等于 $l$，并且 $(a,b)$ 在这条路径上，那么这条边是好边。求好边个数。

跑一下 Floyd 之后，对于一条权值为 $w$ 边 $(a,b)$，把条件列出来，存在 $1 \le i \le q$，满足 $dis(u_i,a)+w+dis(b,v_i) \le l_i$。注意到条件三元组会有 $O(n^2)$，显然不能全部枚举来判断。

移项 $w + dis(b,v_i) \le l_i - dis(u_i, a)$，这个式子的左边固定一个端点 $b$，我们枚举另外一个端点 $v_i$，然后希望预处理右边的最大值来直接判断。此时对于式子的右边就是对于固定的端点 $a$，在所有点 $1 \le u \le n$ 中，取最大的 $l(u,v) - dis(u, a)$。我们提取 $v$ 和 $a$ 作为键，$u$ 是唯一的变元，因此枚举 $u$ 预处理最大值，即可直接判断。

F Exam

给定 $n$ 个串，求有多对串 $(i,j)$ 满足 $s_i$ 是 $s_j$ 的子串，并且不存在 $k$ 使得 $s_i$ 是 $s_k$ 的子串，$s_k$ 是 $s_j$ 的子串。

首先，建出 AC 机，预处理每个点往上走第一个结束节点和 fail 树的 dfs 序。

我们枚举每一个串，计算它有多少个直接的子串。显然直接子串一定是，这个串所有前缀的最长后缀，满足这个后缀在字典中出现过，直接使用 AC 机预处理的信息容易得出（注意，完整串可能需要特判，因为完整串的最长后缀是其本身）。但是这些串中显然会有很多重复的，也会有很多串在另外的当中出现过。

我们结合 AC 机的结构，观察一下哪些串是重复的。显然每个最长后缀对应节点，在 fail 树上到根的路径都是出现过的，这些节点的串构成母串的所有子串。

但是，考虑下面这样的情况：

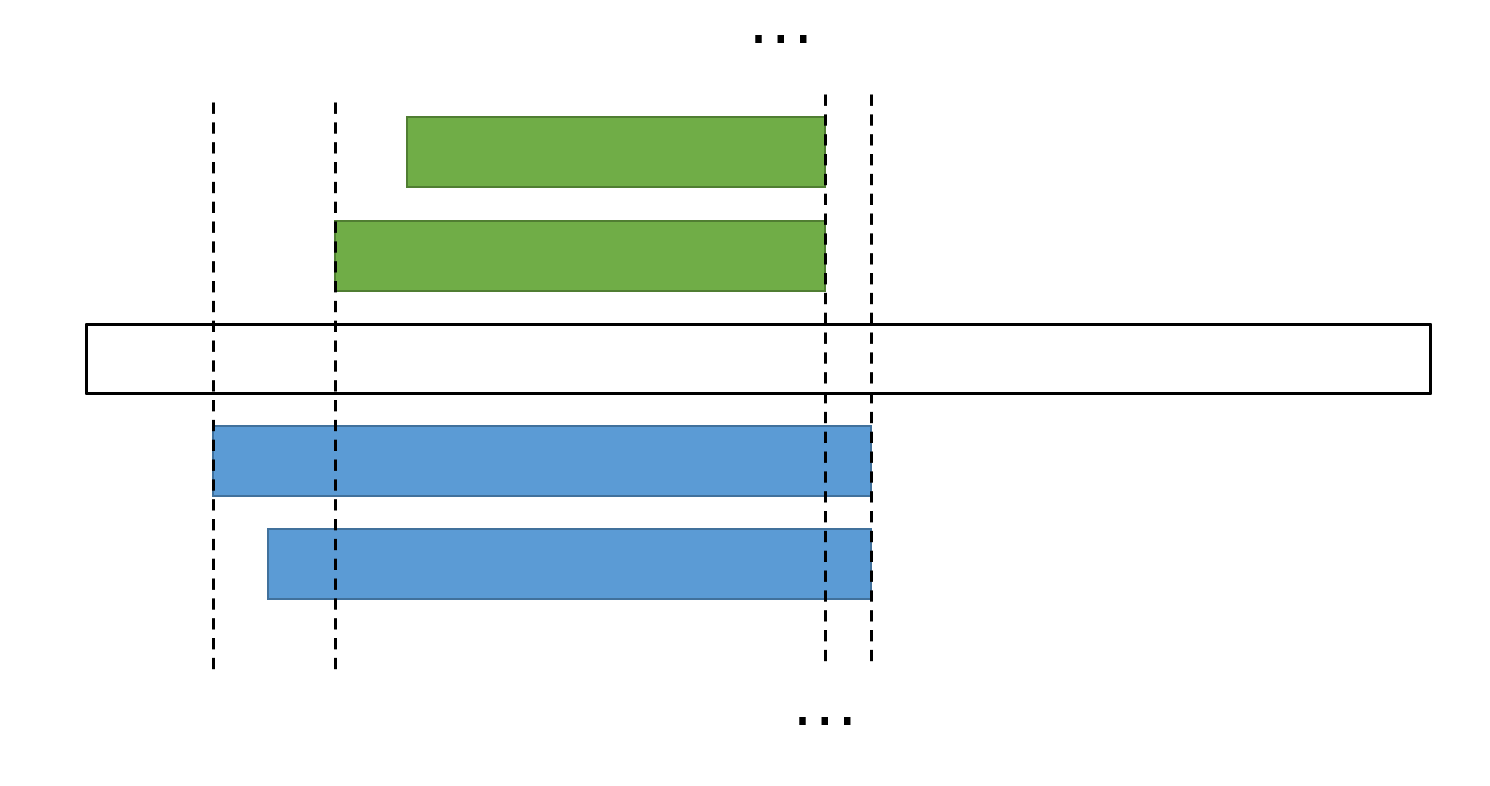
对于那个最长的绿串实际上被包含在蓝串内部，但是根据我们上述的做法，我们多统计了绿串。因为上述做法，只排除了后缀的情况，没有排除不是后缀而是内部的情况。

正确做法是，我们可以通过从右往左枚举右端点，记录单调下降的左端点，将所有左端点变化处作为询问的关键点，这样就能够排除串在内部的情况。

题面

给定一棵 $n$ 个点的树，每个点有权值 $a_i$ 和 $b_i$，定义 $f(x)$ 表示满足 $a_i$ 之和等于 $x$ 的所有树上独立集中，$b_i$ 权值和最大的方案数。你需要求出 $f(1), f(2), \dots, f(m)$ 的值。

其中 $1 \le n \le 50, 1 \le m \le 5000$。

分析

显然有一个 $f(i,j,0/1)$ 的 $O(nm^2)$ 的树形背包做法，无法通过。

我们考虑在 dfs 序上进行 DP，注意到一个点能否被选择只和它到根的链上的状态有关，于是我们按照 dfs 序枚举时，同时记录每种链上的状态的信息。但是，这样仍然难易通过，因为可能会存在一个长链。

对于树进行轻重链剖分，不同于传统的剖分后标号方式，我们首先标记轻子树的 dfs 序，然后标记重子树。对于这样的标号方式，当我们考虑 dfs 序上的第 $i$ 个转移到第 $i+1$ 个时，要么是沿着向下的边走了一步，要么是跳到该重链链头的父亲后，往下走了一步，或者重复往上跳链头的父亲，然后往下走一步。那么，以这样的方式标号后，每个点到根的路径上有用的点，就只有每条重链的底部节点（每条重链链头的父节点）。于是，我们对这些关键点进行状压。

转移时，需要考虑第 $i$ 个点上的关键点集合和第 $i+1$ 个点上的关键点集合的重复部分，得到具体的转移状态，分成使用节点 $i+1$ 和不使用节点 $i+1$ 两种进行转移。

2019 年 CCPC 秦皇岛 G Game on Chessboard

题面

给定一个 $12 \times 12$ 的正方形棋盘，放了黑白两种棋子，每个格子有权值 $w(i,j)$。有两种操作，删除一个棋子 $(i,j)$，花费为 $w(i,j)$，删除一对黑白棋子 $(i_1,j_1)$ 和 $(i_2,j_2)$，并且满足这两个棋子的左下角范围内不能有其它棋子，花费为 $|w(i_1,j_1)-w(i_2,j_2)|$。求删除所有棋子的最小花费。

分析

注意到，每次能够删除的棋子在一条从坐上到右下的轮廓线上，对轮廓线进行状压，$0$ 表示向下，$1$ 表示向右。

轮廓线有 $2n \choose n$ 条，状压枚举时，找到拐角点进行转移。

时间复杂度 $O(n^2 {2n \choose n})$。

2020 年 ICPC 上海 F Fountains

题面

给定一个长度为 $9$ 的序列 $a_1, a_2, \dots, a_n$，求选出 $k=1,2,\dots,\frac{n(n+1)}{2}$ 个不同的子区间时，最大化 $\sum_{L \le R} \max_{i=1}^k [L \le l_i \le r_i \le R] w(l_i, r_i)$，其中 $w(l,r)=\sum_{i=l}^r a_i$。

分析

首先，我们将线段 $[l,r]$ 看成平面上的一个点 $(l,r)$，显然这个点左上角的点对应线段都包含线段 $[l,r]$。

对所有子区间线段按权值由大到小排序，考虑 $dp(i,j,S)$ 表示考虑到了前 $i$ 条线段，选出了 $j$ 个，状态 $S$ 内的所有区间都已经确定了包含的线段，显然 $S$ 是一个从左下角到右上角的轮廓线。当我们枚举下一个放进来的线段时，就和原有状态求一个并，因为排序的缘故，只需要更新没有更新过的点的答案，同时维护出新的轮廓线。

时间复杂度 $O((\frac{n(n+1)}{2})^2 {2n \choose n})$。

题面

依次将 $n$ 个下边界在 $x$ 轴上的矩形涂黑，求每次涂色后总图形的周长。

其中 $1 \le n \le 2 \times 10^5$。

分析

横线部分就是线段覆盖，这是平凡的。

竖线部分，更新操作就是区间取 $\max$，对于线段树节点 $[l,r]$，需要维护 $\sum_{i=l}^{r-1} |a_{i}-a_{i+1}|$。

考虑 Segment Tree Beats，我们在线段树节点维护了区间最小值和区间次小值。当最大值更新为 $x$，$x$ 小于节点次大值，将区间内所有最小值提升为 $x$，可以发现这个过程中改变的是最小值和相邻高点之间的差。因此，我们对于一个线段树节点区间，维护所有相邻的是否是最小值导致间断点，假设我们维护了这样的间断点个数，那么对于区间答案的容易进行更新。

间断点的个数容易维护，首先它可能从左右子树上传得到，然后在考虑将左右区间拼接点的贡献即可。

最后，注意我们区间覆盖最小值时打的标记，也包含了懒标记效果，记得下传信息。注意维护次小值的细节。

题面

给定 $2n$ 个线段 $[l_i,r_i]$ $(1 \le i \le n)$ 和 $[s_i,t_i]$ $(1 \le i \le n)$，对于所有排列 $p$ 求 $\bigcup_{i=1}^{n} [l_i,r_i] \times [s_{p_i}, t_{p_i}]$ （面积并）之和。其中 $1 \le n \le 2 \times 10^5$。

分析

拆开来算贡献。

对于第一维（$x$ 轴），将其通过左闭右开区间离散化为小块。假设每块被覆盖了 $s_i$ 次，也就意味着这一个块对应了 $s_i$ 个 $y$ 轴线段。比如说，$s_i=0$，那么上面没有任何线段；$s_i=1$，对应了 $1$ 个线段，也就是所有线段均有可能竖着放在它上面，对答案的总贡献为所有线段的总长度；类似地，$s_i=2$ 就是枚举一对线段计算贡献之和。

可以发现，对于每一个小块只有参数 $s_i$ 有效。于是，我们将问题转化为了一个一维的问题，即对于从线段集合中选择 $k=0,1,\dots,n$ 条线段产生的总贡献，形式化地 $f(k)=\sum_{S \subseteq U, |S|=k} |\bigcup_{i \in S} [s_i, t_i]|$。

再拆开来算一次贡献，同样离散化。假设每块被覆盖了 $s_i$ 次，这个块产生贡献当且仅当选出的 $k$ 个块包含 $s_i$ 中的某一个，即方案数就是 $\binom{n}{k} - \binom{n-s_i}{k}$，对于贡献还要乘上块的长度。观察上面的式子，第一部分是平凡的，关键是第二部分，因为我们最终计算的是 $f(k)$ 每个点的值，因此同样的 $n-s_i$ 产生的长度贡献可以记录在一起。于是，我们定义这部分的贡献函数 $g(k)=\sum_{i=k}^n a_i C(i,k)$，其中 $a_i$ 就是长度和。

将 $g$ 展开

注意到上式的下标分别为 $i$ 和 $i-k$，即差为定值 $k$，使用 FFT 计算即可。

最后，还有一点小问题，$f(k)$ 的贡献是无序的。它表示从第二个集合中选择了 $k$ 条线段去和横轴某一小块的 $k$ 次覆盖对应，剩余随便，也就是需要乘上两部分内部的排列，即 $k! \times (n-k)!$。