2021 Shandong Provincial Collegiate Programming Contest
A Beta Go
题面
给你一个 $n \times n$ 的只包含白子的围棋棋盘,你执黑子按照正常围棋规则下(题面包含所有需要的知道的规则),白子只会 pass,求你能吃多少白子。
题解
根据第一个样例,容易注意到白子的吃子是会有一些依赖关系,然后已经放下的黑子不会影响之后继续吃白子(一定有气)。
直接使用迭代算法,每次找一块能吃的白子吃掉,复杂度不会超过 $O(n^4)$,但是好像没法卡满,一个能卡到 $O(n^3)$ 的数据是,类似以下这样,$1000 \times 1000$,包含 $500$ 个竖着的白棋。
1 | O.O. |
但是我们没必要每轮迭代扫一遍找可以吃的块,可以直接把白子连通块和棋盘空余连通块之间的依赖关系抠出来。
具体地,就是如果一块白子的某一部分气,占满了某个棋盘空余连通块,那么这个连通块至少得留一个位置,才能符合规则,因此连一条这个空余连通块到白子连通块的边。
花费 $O(n^2)$ 或者 $O(n^2\log n)$ 的时间连出边,跑一个拓扑排序的类似物即可。注意,这里与拓扑排序的区别是,只要剩了一条边就可以扩展,不用全部清空入边。
时间复杂度: $O(n^2)$ 或 $O(n^2\log n)$ ,根据实现方式的不同。
B Build Roads
题面
给定一个 $n$ 个点的无向完全图,$i$ 和 $j$ 之前的边权是 $\gcd(a_i, a_j)$,保证数组 $a$ 随机,求 MST。
题解
考虑素数分布,int 范围内两个素数之间的最小间距不到几百,而如果随出来的数组里有素数答案就是 $n-1$ 了,所以 $[L,R]$ 范围很大时答案就是 $n-1$。范围很小的时候暴力一下就行了。还需要稍微注意一下 $L=R$ 的情况。
非常抱歉,出题人和验题人在做的时候没有考虑到直接输出 $\gcd(a_1, a_2,\dots, a_n) \times (n-1)$ 的情况。首先 $n$ 比较大的情况下很难随机出问题,所以是没问题的。并且我们造数据的时候,小数据并没有随机很多,导致出现了这样问题,向大家表示抱歉。
Hack 参数:5 11 15 1256。数组是 14 15 14 14 12,答案是 $5$。
C Cat Virus
题面
给定一棵树,黑白染色方案,满足一个黑点的子树都是黑点,白点任意。
你现在构造一棵树,使得它的染色方案数为 $K$。
题解
首先考虑怎么数,令 $f(u)$ 表示子树黑白染色的方案数($u$ 是白色,染黑色方案是 $1$),转移方程是 $f(u) = 1 + \prod (f(v)+1)$。
假设 $K$ 是奇数,那么 $K-1 = 2^l \times K’, l \ge 1$,连一堆单点之后 $K$ 缩小了一半。
假设 $K$ 是偶数,连单个儿子变成奇数的情况。
最后,$1 \le K \le 10^{18}$,大概至多 $110$ 多个点。
D Dyson Box
题面
二维空间里放了 $n$ 个盒子,有水平往左和竖直往下两种重力,求重力作用之后形成的轮廓周长。
题解
横竖是对称的,考虑做竖直的情况,令 $h(i)$ 表示第 $i$ 列上的盒子个数,答案就是:
$$
\sum [h(i)] + \sum |h(i) - h(i-1)|
$$
每次添加盒子,第一部分求和容易维护,第二部分至多只会影响左右两个,都可以 $O(1)$ 更新答案。
时间复杂度:$O(n)$。
E Evaluate Expression
题面
给定一个包含数字,$+$,$\times$,$()$ 的表达式,只有不同运算符和括号之间的优先级,同级运算没有结合律。求表达式求值的方案数。
题解
将表达式 parse 成一个多叉树(递归下降,栈等等)。
考虑树形 DP,$f(u)$ 表示子树 $u$ 的求值方案数,$siz(u)$ 表示子树 $u$ 内部的运算符个数。
对于一层,也就是将每个子树内部的运算符和这一层同级的所有运算符混合在一起,求一个方案数。
首先,每个子树内部的顺序的方案数 $f(son)$ 最后乘在答案里即可,也就是每个子树实际有用参数只有 $siz(son)$。
然后因为同级的运算符之间没有任何顺序,同级可以使用任意顺序,只需要满足这个运算符,在它对应的左右子树内部所有运算符之后。
首先考虑 $O(n^3)$ 的做法,直接区间 $DP$,$g(l,r)$ 表示第 $l$ 个孩子到第 $r$ 个孩子之间的方案数。转移需要枚举,这个区间最后一次运算符在哪,大概是 $\sum_{i=l}^{r} g(l,i) \times g(i+1,r) \times \text{左边 $i$ 个运算符保序地插入右边}$,最后一部分是一个和运算符大小有关的组合数。
然后,标程的做法是 $O(n^2)$ 的,不考虑同级的运算顺序,实际上只需要满足上面那个序的限制。令 $f(i,j)$ 表示考虑到了 $i-1$ 和 $i$,并且子树 $i$ 内的最后一个运算符的位置在 $j$。转移就是考虑第 $i+1$ 个运算符,枚举子树 $i$ 和子树 $i+1$ 中间那个运算符的位置,这一部分可以通过前缀和,优化到 $O(n^2)$ 进行转移。
最后时间复杂度是 $O(n^2)$。
F Birthday Cake
题面
给定 $n$ 个串,求有多少对串能拼出平方串(能够表示成两个相同的字符串连接在一起的,即 $AA$)。
题解
首先,有一个结论若 $AB$ 是平方串,那么 $BA$ 也是平方串,所以只要正着做一次就行了。
枚举所有串,对应下图的蓝色部分,在枚举下图的橙色部分,最后需要在所有串中查询绿色部分的出现次数。
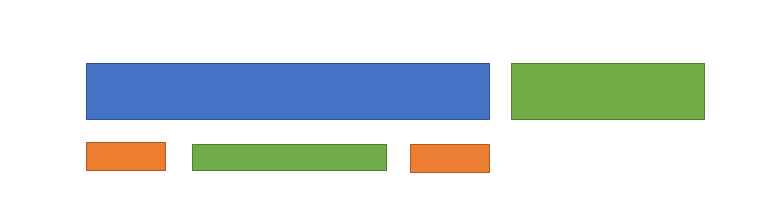
使用哈希或 KMP 等字符串算法容易实现。
请注意哈希的一些细节:自然溢出可以直接卡掉 Anti-hash test. - Codeforces,造数据的时候卡了部分常见的模数和 base,没过可能是和出题人心意相通了或者其它地方写挂了。
G Grade Point Average
题面
输出 $\sum_{i=1}^n a_i / n$,保留小数点后 $k$ 位(直接截断后面的)。
题解
模拟一下除法的过程。
H Adventurer’s Guild
题面
Yuna 的生命值是 $H$,体力值是 $S$,有 $n$ 个任务,每个任务有生命值和体力值的花费。生命值不能降到 $0$ 或 $0$ 以下,体力值的多余消耗会算到生命值里。求最大任务收益。
题解
二维背包 $f(i,j)$ 表示剩余生命是 $i$,体力是 $j$ 的收益。考虑加一部分的转移,当 $j < s$ 时,把多余的体力值消耗扣到生命值里。
I Chemical Code
题面
维护一个长度为 $n$ 的字符串 buffer,每次会往里面加数组,CHO,或者加一对括号(不会破坏的已有的括号匹配),询问相对分子质量,模 $3^2 \times 7^3 \times 319129$。
题解
维护两棵线段树,分别表示每个位置的系数和每个位置对答案的贡献。
插入一个 CHO:
- 若插入位置的后继是一个数字,那么需要找到这个位置的前驱,单点或者区间(括号)的系数和贡献做一个除法,然后更新当前点的系数;
- 将对应位置的贡献改成数字乘上系数。
插入一个括号的过程类似于 CHO。
插入一个数字(题目保证不会有连续数字):更新它的前驱的系数和答案贡献。
最后,把前面这一堆情况判好了之后,就是需要实现区间乘法,除法,维护区间和。
除法不太好弄,考虑 CRT,计算模 $p^k$ 下的答案,这里线段树只需要维护区间和是 $p^k q$,其中 $p$ 不整除 $q$。注意到因为我们的操作过程,除法一定是能除的,区间除法就是先减小 $k$,然后除掉逆元。
时间复杂度 $O(n \log n)$。
K Piggy Calculator
题面
定义新运算 $a \odot^k b$ 是 $(a+b)\times k$,给定这样一个长度为 $n$ 的只包含新运算的算式,优先级就是 $k$ 的大小,左结合。每次询问一个区间的算式结果。
题解
对 $k$ 按优先级和结合律键建立一棵笛卡尔树。
注意到:笛卡尔树上的 $k$ 值满足小顶堆的性质,而位置满足二叉搜索树的性质。
预处理每个子树计算表达式的值。

首先用 LCA 找到区间 $[L,R]$ 的最小值位置,也就是这一个子表达式的最后一个运算符,我们考虑求出它的左右表达式的值。
左右是对称的,以做右边为例:假如我们现在要找 $[5,6]$ 这个区间在 $4$ 号点左边的值。显然,$6$ 号点到根的路径上有一些点是在区间外的,根据二叉搜索树的性质,$6$ 点往上爬,当某一个条父边是父节点的右子树,那么这个父亲就是当前节点的前驱。
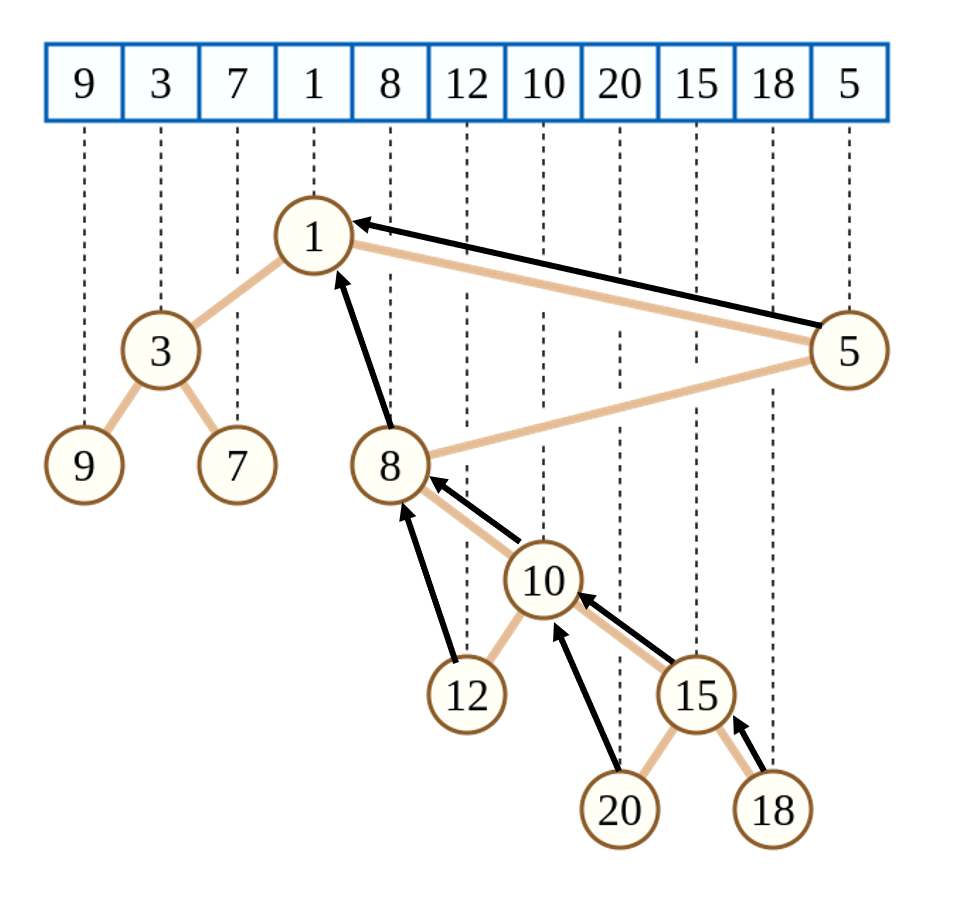
在笛卡尔树上 dfs 可以扣出这样的前驱关系,显然它也满足树的结构。并且我们在计算询问表达式的值的时候,不需要用到右边界右边的表达式,而只需要使用那单个值,这个值会传递到它的前驱上,和这个前驱的左子树合并计算(已经预处理了)。
但是前驱跳的次数还是无法接收,这里可以直接倍增前驱关系树上的一次函数。
询问时,也倍增合并一次函数。左边也是类似的。
时间复杂度 $O(n \log n)$。
L Construction of 5G Base Stations
题面
一个长度为 $n$ 的街道,每个整点上有一个人,有 $m$ 个基站,每个基站的连接概率为 $p_i$。
每个人,都会按照由近及远,先左后右的顺序依次尝试连接基站,成功连接基站 $i$ 的概率是 $p_i$,如果都失败了,那么重新再来一遍。
每个基站的开销是连接人数的平方。求期望运行总代价。
题解
令 $F = \prod (1 - p_i)$,输入保证这个式子模意义下不是 $1$。
考虑人 $i$,连到基站 $x$ 的概率:
$$
\frac{p_x}{1-F} \prod_{\text{连接 $y$ 更近}} (1-p_y)
$$
先只考虑代价是人数,那么一个站 $x$ 的期望人数就是:
$$
\frac{p_x}{1-F} \sum_{i=1}^n \prod_{\text{$i$ 连接 $y$ 更近}} (1-p_y)
$$
关键是后面这个式子,左右堆成,以左半部分为例:
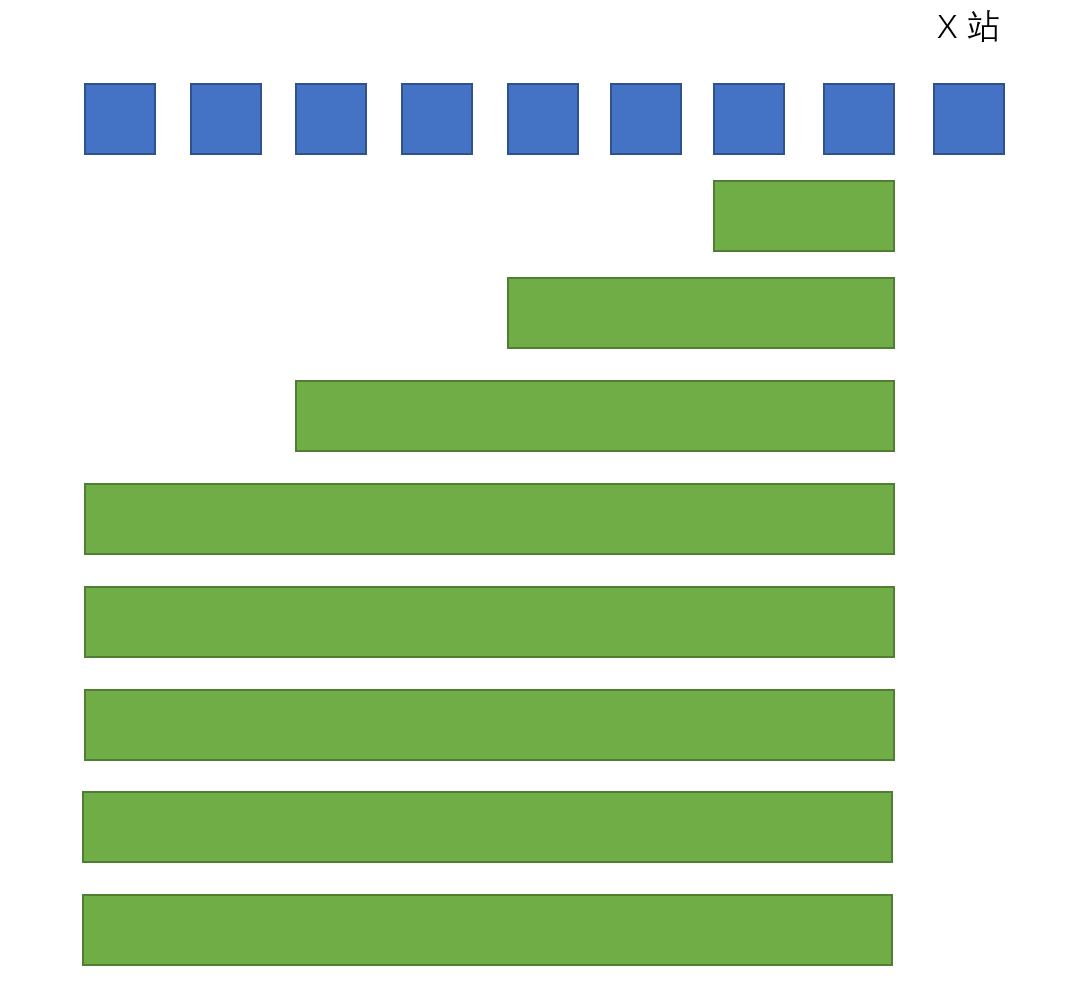
每个绿条是代表左边每个人的概率连乘包含的部分,考虑 $x$ 往左两个位置,相当于全部乘上新的格子的概率,在补上两个漏掉东西。
可以分奇偶 $O(n)$ 前缀和后缀和实现。
最后,考虑贡献的是平方,也就是考虑一对人出现连接到 $x$ 站的概率,相当于求:
$$
E(X^2) = \sum_{i \neq j} P(i) P(j) + \sum_{i=1}^n P(i) = (\sum_{i=1}^n P(i))^2 - \sum_{i=1}^n P^2(i) + \sum_{i=1}^n P(i)
$$
上面所有的式子全部都平方一下,前缀和转移的时候也平方一下,就能求出 $\sum_{i=1}^n P^2(i)$。
时间复杂度:$O(n)$。
M Matrix Problem
题面
给定 $0 / 1$ 矩阵 $C$,构造两个矩阵 $A,B$,其中 $1$ 形成了完整的不分散的一块四连通块,并且对于 $C$ 中所有位置,若是 $1$,则 $A,B$ 对应位置必须都是 $1$,否则 $A,B$ 之中必须有一个这个位置为 $0$。
保证 $C$ 阵的边框都是 $0$。
题解
一种构造方法,样例的答案是:
1 | 11110 |
$A$ 最左边一列是 $1$,$B$ 最右边一列是 $1$,然后行分奇偶全染成 $1$。