题面

给定一棵有根树，每个点的权值为 $a_i$，每个时刻所有权值大于 $1$ 的点，权值减一，然后同时将每个点的权值爬到它的父亲上，根节点就加到最终答案上。

其中 $1 \le n \le 2 \cdot 10^5$。

来源：第 18 届上海大学程序设计联赛 G 血压游戏

分析

显然不同层的结点不会相互影响，若只考虑同一层的结点，那么题目中的过程可以直接模拟。

对同一层的结点建一棵虚树跑一下即可。

题面

给你一个病毒，他的强度为 $x$，你不知道 $x$ 的值，但是你知道它在 $n$ 个区间中的某一个 $[1, a_1],[a_1+1, a_2], \dots, [ a_{n-1} + 1, a_n ]$。

你现在有 $m$ 种操作，第 $i$ 个操作是强度减少 $w_i$，花费 $v_i$。你需要通过操作将病毒强度控制到区间 $[1, a_1]$ 中。

你现在要求 $x$ 是 $[1, a_n]$ 中等概率取一个的最小的花费期望（答案乘 $a_n$ 变成整数）。

其中 $1 \le a_n, m \le 2000$。

分析

显然病毒通过一系列操作病毒的强度一直是数轴上的某一段区间，我们令状态是 $f(l,r)$ 表示病毒强度在 $[l,r]$ 范围内的最小的花费期望。

如果 $[l,r]$ 在第一个区间内，则花费为 $0$。

如果 $[l,r]$ 没有跨越任何区间，则枚举下一次操作的花费进行转移。

如果 $[l,r]$ 跨越了区间，则用原来的分段点，将区间分段，每段单独算再加起来。

显然一共有 $n^2$ 种状态，转移是 $O(m)$ 的，时间复杂度是 $O(n^2m)$。

但是，我们考虑 $[l,r]$ 跨越区间的情况，它是由一堆连续的完整区间，开头的一个完整区间的后缀和结尾的一个完整区间的前缀组成。我们转移时实际上是将当前区间向左平移了一段距离，如果该区间平移后没有发生跨越，那么这个区间的转移还要继续重复枚举所有操作，产生了冗余。当一个区间产生了跨越后，这个区间的计算就会被拆解成上面的段，不再是简单地枚举操作。

因此，我们对 $[l,r]$ 区间进行转移时，强制钦定他转移到跨越的情况（或者某个区间的前缀或后缀，或者到状态一）。两头的区间我们使用记忆化搜索进行转移，而中间的完整区间可以用前缀和直接算出来。所以总体状态数就是 $O(a_n)$。

时间复杂度：$O(n^2)$。

A Bad Ugly Numbers

输出 $233333333$。

B Maximums

注意到 $a_1=b_1$，扫一遍。

C Permutation Partitions

给定一个排列，将其分为 $k$ 个连续段，每段的权值是该段的最大值，求划分的最大权值和方案数。

显然就是取最大 $k$ 个即可，划分就是枚举分界点，方案数乘起来即可。

D Prefix-Suffix Palindrome

给定一个串 $s$，找一个最长的回文串 $p$，使得 $p=a+b$，其中 $a$ 为 $s$ 的前缀，$b$ 为 $s$ 的后缀。

枚举前后缀的相同的长度，在中间找一个以某个位置开头或结尾的长度小于一个值的最长回文串，抄一个回文树就赢了。

E Bombs

给定一个排列 $p$，有另外一个排列 $q$，对于 $q$ 的每个前缀，将对应位置设置上炸弹，求对应的权值。

维护一个集合 $S$，从左到右扫描排列 $p$，加入集合，如果是炸弹就删除集合的最大值，最后留下来的最大值就是权值。

显然，答案是单调不增的。因此，只需要检查答案能否减小。

答案减小必定是炸掉最大的那些数字。如果我们无视一些炸弹的顺序，实际上对于要被炸掉的关键位置，就是和它之后的所有炸弹连边。这样建图后，就是判断是否存在完美匹配。

考虑 Hall 定理，判断条件等价于，对于最后一个位置，其后缀炸弹总数大于等于 $1$，倒数第二个后缀炸弹总数大于等于 $2$，以此类推。

使用线段树维护后缀和的最小值即可。

F Wise Men

给定一个 $n$ $(2 \le n \le 18)$ 个点的无向图，一个排列可以生成一个 $0/1$ 串，如果第 $i$ 个和第 $i+1$ 个有边则是 $1$ 否则为 $0$。对于所有长度为 $n-1$ 的 $0/1$ 串，求它对应多少个排列。

首先将问题转化为高维后缀和，令 $f(S)$ 表示状态为 $S$ 的方案数，其中 $S$ 内的 $1$ 表示有边，$0$ 表示无边或有边。最后做一个高维后缀和的差分就能弄出真实答案。

注意到一个结论，对于一个状态 $S=110111$ 只需要看每个 $1$ 连续块的 $1$ 个数加一的多重集合，这里是 ${ 3, 4 }$（中间那个连接处没有考虑，因此也可能是 $111111$）。

因此只需要枚举 $n$ 的整数划分方案就能搞出每个 $f(S)$ 的值，并且注意到 $P(18)=385$。

状压 DP 搞出每个子集作为链的方案数，令状态是 $dp(i,S)$ 表示链头为 $i$，点集为 $S$ 的方案数，时间复杂度 $O(2^nn^2)$。

记全集为 $U$，$g(i,S)$ 表示选出点集 $S$，$i=|S|$ 的方案数，我们要求的是

$$f(S)=\sum \prod_{i=1}^k g(|s_i|,s_i)$$

其中 $ \sum_{i=1}^k |s_i| = n, \cup_{i=1}^k |s_i| =U $，实际上 $ { |s_1|, |s_2|, \dots, |s_k| } $ 就是 $S$ 对应的整数划分方案。同时，这个卷积的式子也保证了一个点不会出现多次，因为一个点出现多次的话，必定不能满足整数划分的条件。

枚举到一个整数划分 ${ a_1, a_2, \dots, a_k }$ 后，也就是对 $g(a_1,0 \dots 2^n), g(a_2, 0 \dots 2^n), \dots$ 全部做一个子集或卷积。预处理 $g(1), g(2), \dots$ 的点值后，在搜索时顺便乘起来，在枚举完后就得到上面整个卷积的点值表示 $A$。由于最后我们只需要 $U$ 处的系数，可以直接使用 $O(2^n)$ 的容斥得到 $U$ 处的系数。

$$
FWT^{-1}(A)[x^U] = \sum_{s \in U} (-1)^{ |s \oplus U| } A[x^s]
$$

搜完整数划分，求出每个点集 $S$ 的 $f(S)$ 值后，做一个高维差分，把高维后缀和转化为真实值即可。

时间复杂度：$O(2^n(P(n)+n^2))$，其中 $P(n)$ 表示 $n$ 的整数划分方案数。

一个优化常数的建议：搜整数划分时，剪掉不合法的分支，不去乘点值。

A Two Rabbits

B Longest Palindrome

给你 $n$ 个长度为 $m$ 的串，你挑一些出来构造一个最长的回文串。

注意到是每个串长度相同，所以一定是两两配对，加上中间可能会有一个回文串。

C Air Conditioner

你有一个权值，你每天可以选择把他 $+1,-1$ 或者不变，有 $n$ 个条件，第 $t$ 天，权值范围在 $[l_i,r_i]$ 中。

维护一下你的权值的范围即可。

D Shortest and Longest LIS

你有长度为 $n-1$ 的 $<$ 和 $>$ 组成的串，表示 $a_i$ 和 $a_{i+1}$ 的大小关系，你现在需要构造出 LIS 最大和最小两个排列。

我的构造方式过于复杂，以致于没来得及交上去（呲牙）。

一种简单的方式，以 LIS 最小为例，你肯定希望整体是在往上走的，因此对于小于号，权值 $+\infty$，大于号权值 $-1$，这样你每次都是往上升的状态，最后每个值必定不同，离散化即可。LIS 最大，考虑整体往下即可。

E 1-Trees and Queries

你有一棵无根树，$q$ 次询问，独立连一条 $x$ 到 $y$ 的边，询问 $a$ 到 $b$ 是否存在一条长度为 $k$ 的路径，路径可以随意走，可以走重复的点或边。

有 $3$ 种路径，$a \to b$，$a \to x \to y \to b$ 和 $a \to y \to x \to b$，只需要满足长度不超过 $k$，且模 $2$ 同余即可。

F Animal Observation

给你一个 $n \times m$ 的网格，每行最多选一个长度为 $k$，高度为 $2$ 的矩形（往上延伸一格）（特别地，最后一行可以只选一行），求最大的选中权值和。

加一个空行，简化一下变成 $2$ 到 $n+1$ 行。记 $dp(i,j)$ 表示在第 $i$ 行选择 $j$ 开始的那个矩形的最大权值。

转移分成 $3$ 个部分，首先在所有与左下角是 $(i,j)$ 的矩形没有交的的位置的 $dp$ 值，取一个 $\max$。

剩下两个部分是左边相交和右边相交，两种类似，下面讨论右边相交的情况。($Rect(i,j)$ 为这个位置的矩形权值)

$$
dp(i,j) = Rect(i,j) + \max_{i \le j < i + k}(dp(i-1,j) - \sum_{k=j}^{i+k-1} a_{i-1,k})
$$

将上述转移用前缀和差分后，实际上就是一个滑动窗口取 $\max$ 的问题，单调优化即可。

问题

维护一个一次函数的集合 ${ f | f(x) = ax+b }$，对于 $x$ 查询集合内最大的一次函数值，另外还需要支持高效的插入一个一次函数。

实际上就是通常所说的斜率优化 DP，在问题 1083E - The Fair Nut and Rectangles 中，对矩形排序后有显然的转移方程：

$$
f(i)=x_iy_i - a_i + \max_{0 \le j < i} (-x_j y_i + f(j))
$$

做法

把一堆一次函数画出来，实际的最值直线构成一个下凸包（下图加粗部分）。

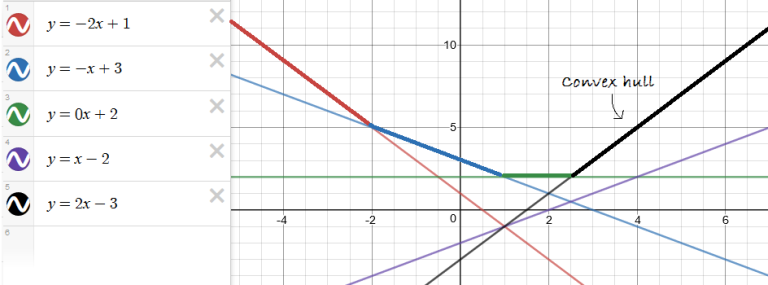
下凸包由一堆从左到右斜率递增的线段（射线）构成。

在上述问题中，有一些具体的性质，插入的斜率 $-x_i$ 是递减的，询问的横坐标也是递减的。

因此，我们可以从右往左地直线加入凸包，又根据询问的单调性，凸包最后超出当前询问点的部分也是无效的。

我们考虑使用双端队列来维护这个凸包，在枚举当前是第几个矩形时：

询问：左移询问点，删除凸包后面无用的部分，找到最佳位置，计算 dp 值；

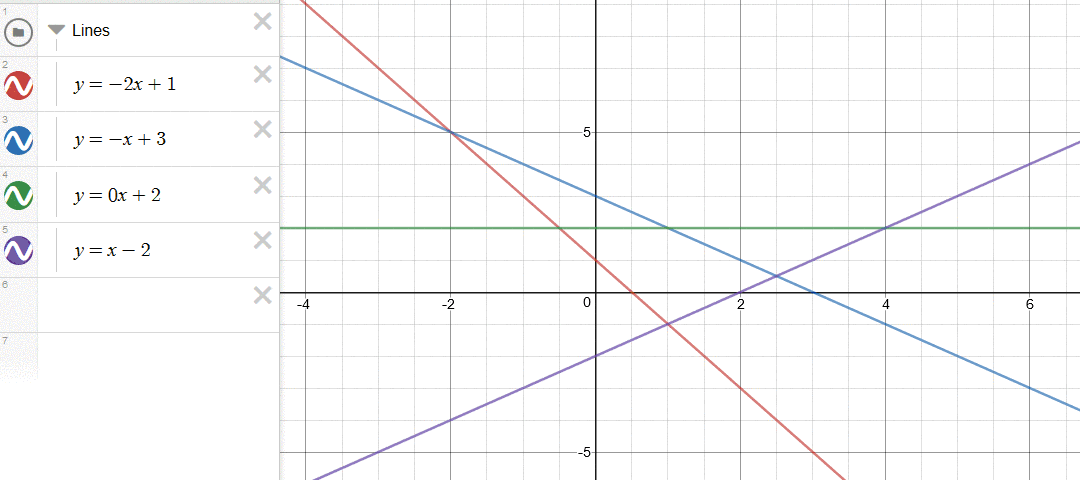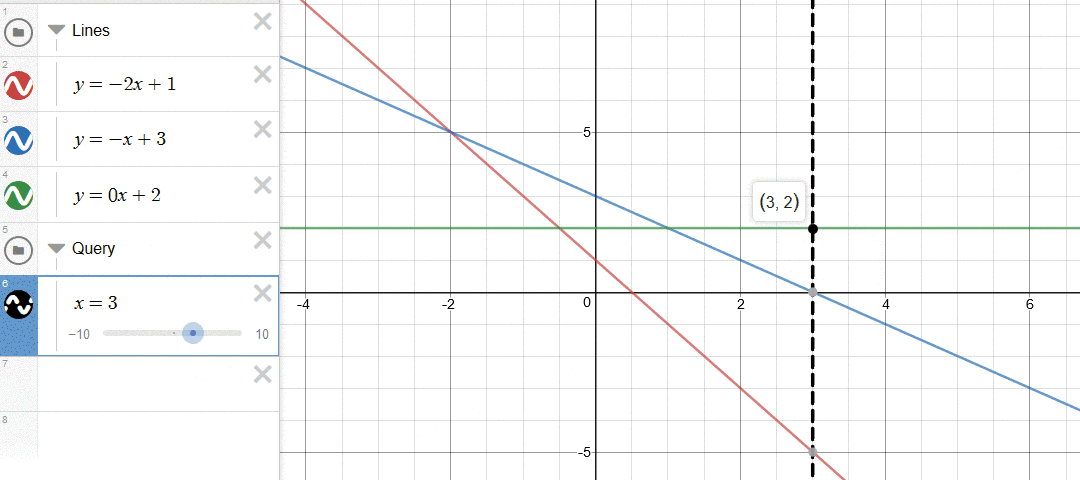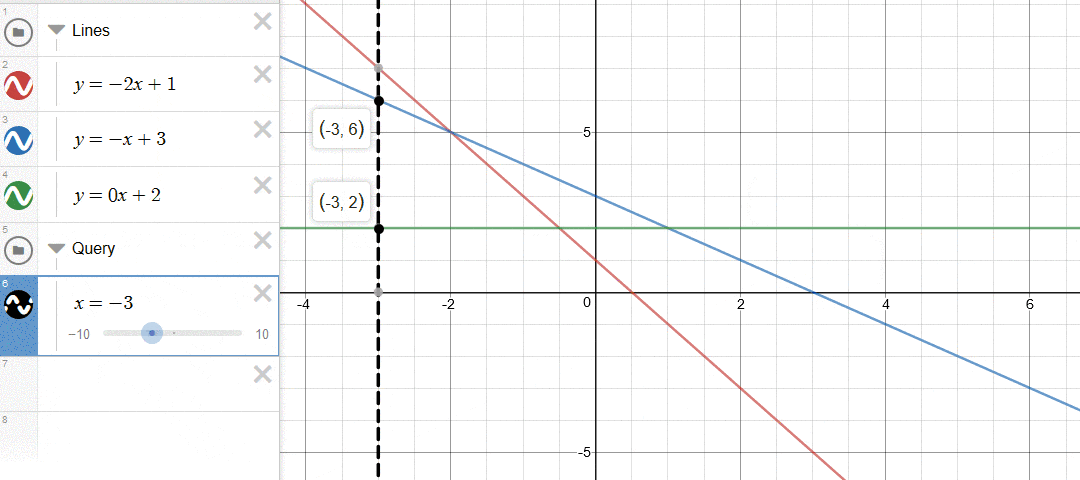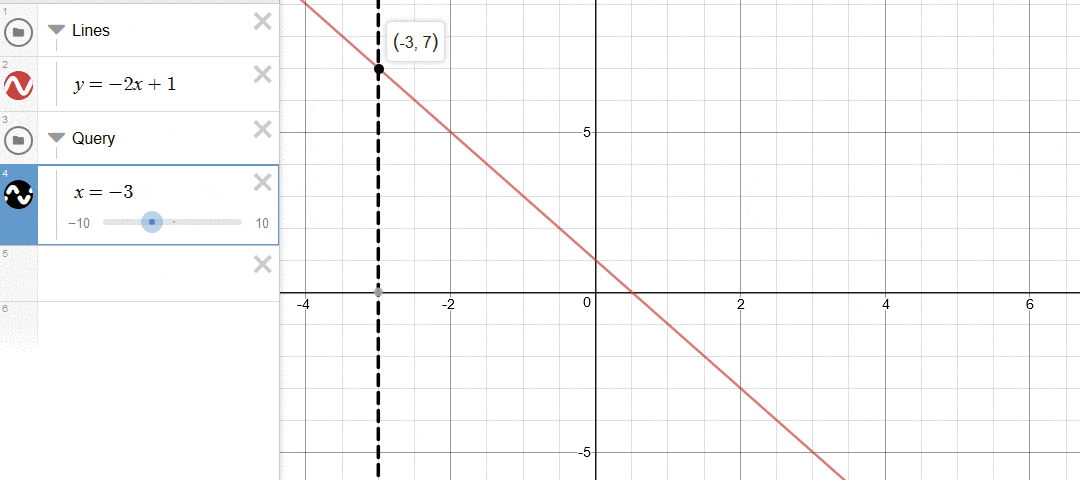
插入：向左加入一条新的线段。注意：虽然我们保证了斜率的单调性，但是仍然会出现新加入的直线完全在原有最左边之上的情况。

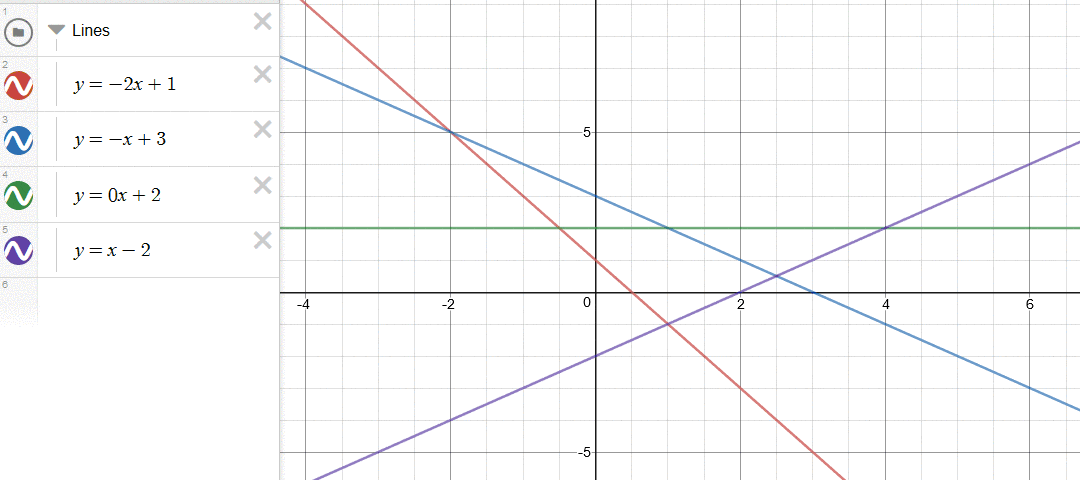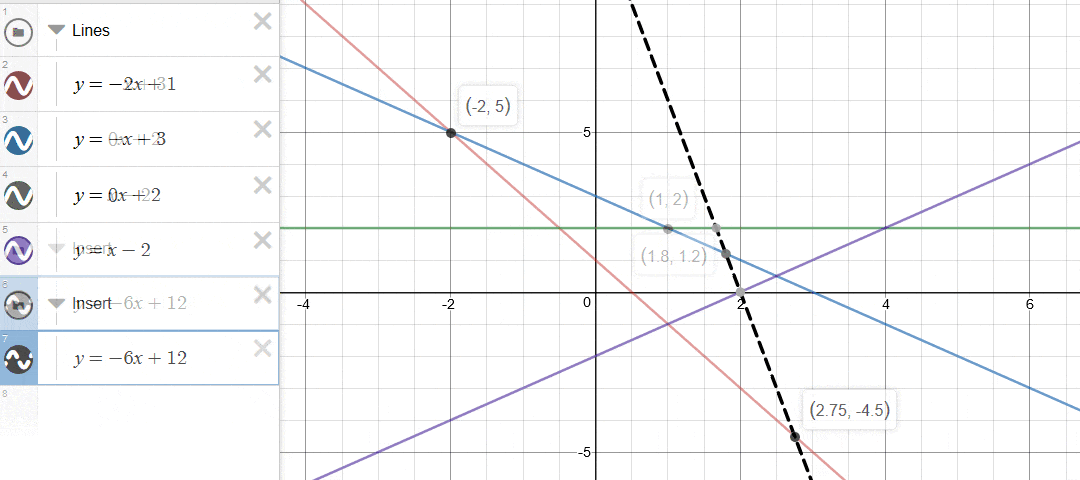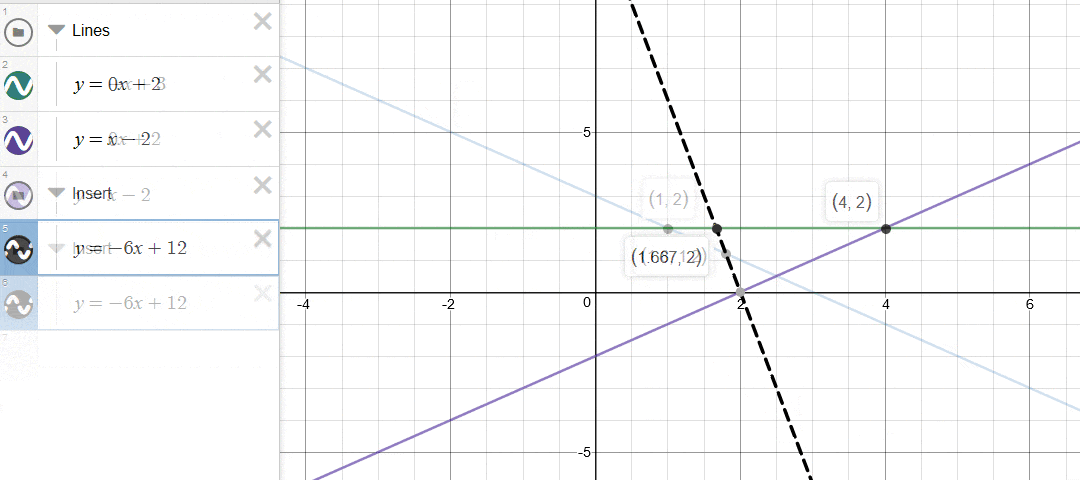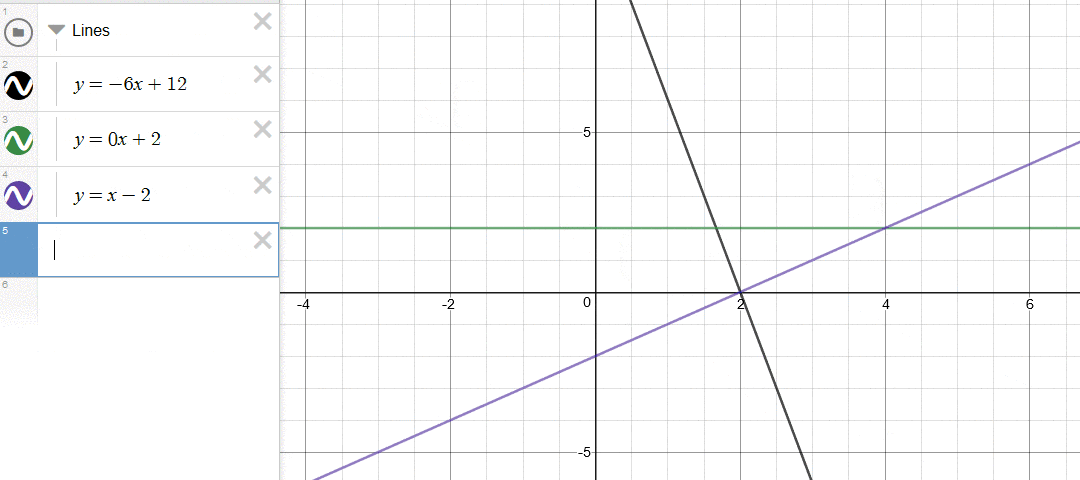
如下图所示，一个简单的判断方式是看两个直线交点的左右关系。在本文中，如果新加入的直线与凸包上最左边的直线的交点，在原有的最左边的交点的右边，那么说明新加入的直线完全盖住了最左边的直线，因此需要删除。

推广

插入斜率有序，询问点任意

仍然按照上述方式维护凸包，询问时通过二分找到该点属于凸包中的哪一段。

插入任意，询问任意

动态凸包，一个简单的实现的是使用 std::multiset，也可以使用 李超树。

多种实现的比较：比较。

转载翻译自 [Tutorial] Convex Hull Trick — Geometry being useful

问题描述

给定 $n$ 个长度均为 $m$ 的字符串，现在你开始投骰子，有 $P_c$ 的概率投出字符 $c$，求第一次出现的串是第 $i$ 个的概率。

一般做法

对这个字符串集合建出 Trie 图后，问题等价于给定一些终点的无向图随机游走问题。

令结点数为 $s$，建出概率转移矩阵后，实际上只有 $s-1$ 条有效的方程，因为无法转移到根节点。但是，随机游走必定会在某个时刻终结，也就是走到所有终止结点的概率和为 $1$。添加这么一条方程后，高斯消元，即可解出在每个终止结点结束的概率。

时间复杂度：$O(nm|\Sigma|+n^3m^3)$。

加强做法

令概率生成函数 $[x^k]G(x)$ 表示在 $k$ 时刻尚未停止的概率，$[x^k]F_i(x)$ 表示在 $k$ 时刻末尾是第 $i$ 个串的概率。

我们要求的就是 $F_i(1),F_i(2),\dots, F_i(n)$。

考虑在每个尚未停止的时刻，往后走一步的情况，即 $xG(x)$，再加上初始时的概率 $1$，这时要么在此处迎来某个串的结束，要么尚未停止，有下式。

$$
1+xG(x)=G(x)+\sum_{i=1}^n F_i(x)
$$

记 $P(S)$ 表示一个串的出现概率，即 $P(S)=\prod_{i=1}^{|S|} P_{S_i}$

对于每个串 $i$，在一个未终止时刻，往后加第 $i$ 个串，即 $G(x)P(s_i)x^m$。这时情况很多，因为加这个串的时候可能中途出现已经终止的情况，设第 $j$ 个串在新加串的 $k$ 位置终止，因此 $s_i[1 \dots k]=s_j[ m - k + 1 \dots m]$，即第 $i$ 个串的前缀等于长度为 $k$ 的第 $j$ 个串的后缀，此时的概率生成函数就是 $F_j(x)P(s_i[k+1 \dots m])x^{m-k}$。

我们枚举每个串 $j$ 和它的前缀长度 $k$，有下式：

$$
G(x)P(s_i)x^m = \sum_{j=1}^n \sum_{k=1}^m [ s_i[1 \dots k]=s_j[ m - k + 1 \dots m] ] F_j(x)P(s_i[k+1 \dots m])x^{m-k}
$$

结合我们要求的，带入 $x=1$，可以得到 $n$ 个方程，但是 $G(1)$ 也是未知量，因此有 $n+1$ 个未知量，联立 $\sum_{i=1} F_i(1)=1$，即可得到 $n+1$ 个方程，高斯消元。注意这里我们的变量数是 $n+1$，不是一般做法的最大 $nm$。

时间复杂度：$O(n^2m+n^3)$。