| rank | solved | A | B | C | D | E | F | G | H | I | J | K |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 27 | 10 | Ø | O | O | O | O | O | Ø | Ø | O | . | Ø |
B
Solved by ytriayggg and XLor (01:57:13, +1).
由于每次操作后,图联通,因此如果把图补成完全图,那么每条边的权值都固定,因此问题转化为异或最小生成树。
C
Solved by ytriayggg (04:05:06).
二维生成函数。
D
Solved by miaojie (02:16:38, +1).
枚举原排列的循环移位,对每个求 LIS。
E
Solved by XLor (01:01:54, +1).
答案是环长的 $lcm$,且答案远小于取模的模数。
F
Solved by miaojie (00:11:39).
签到。
G
UpSolved by XLor.
问题是要求 $\text{mex}$,考虑二分答案后,使用二分图匹配判断是否流满。
但是,我们不能暴力的去建出二分图,对建图进行优化。
首先,我们考虑对每种颜色建出虚树,那么一条边就对应原树的一条垂直树链,这条链上任取一个点都会产生颜色树乘子树关键点数的值,因此需要将这条路径的所有点连向某个值。
然后,这里给一个 $O(n)$ 个点,$O(n\log n)$ 条边的建图方式。第一部分,考虑对树轻重链剖分,每个点拆分为本来的点,连向它在重链上的副本,并将这个点连向重儿子在重链上对应的点,第二部分,对剖分后的 dfs 序使用线段树优化建图。因此,每条垂直树链就可以分为一系列重链(到链顶端),加上一段 dfs 序连续区间。
第一部分的建图,如下所示。可以注意到,若一个点往外有流量时,这个点所属重链的所有祖先结点也可以通过这条流量。
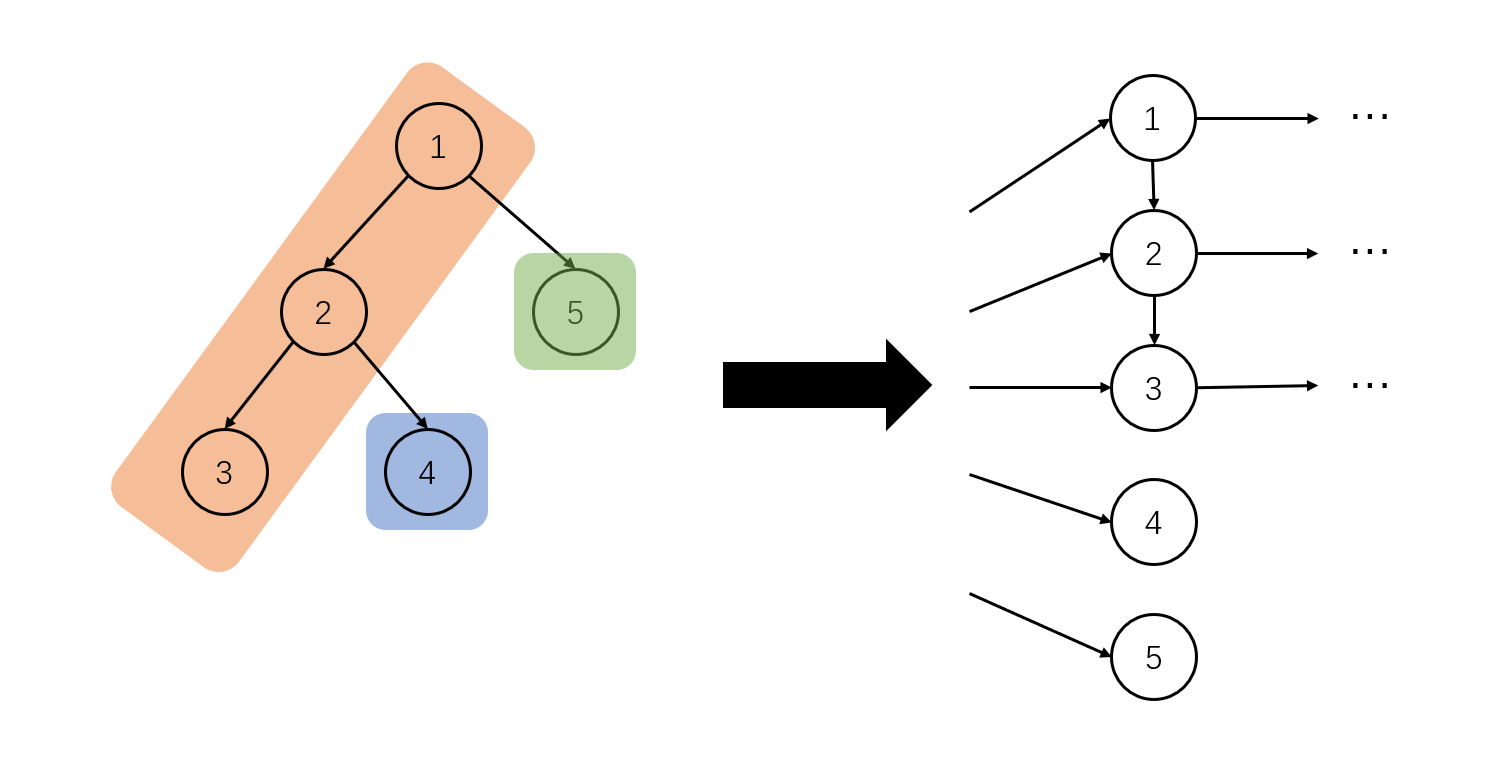
因为,一条垂直树链至多有 $\log n$ 条重链,因此这部分至多会创建 $O(\log n)$ 条边,而线段树一次区间询问至多由 $O(\log n)$ 个区间组成,因此总边数为 $O(n\log n)$ 的。
将图建出来后,二分答案时,不需要每次重新跑一边最大流,如果 $mid$ 成立,那么可以继续在它的残量网络上继续跑,否则撤销本次操作。
H
UpSolved by XLor (-9).
类似于 $\gcd$ 的结论,每个左端点开始至多只有 $30$ 个不同的值,抠出每种值的区间,不妨记为 $(l_1,r_1),(l_2,r_2),\dots$,询问区间包含任意一个答案 $+1$,如果包含了两个,例如 $(l_1,r_2)$ 答案需要 $-1$,以此类推,整理出贡献的点,直接二维数点即可。
I
Solved by miaojie (00:31:52, +1).
K
UpSolved by XLor (-1).
首先,预处理出两个串分别是什么,考虑 $dp(i,j)$ 表示用了第一个串的前 $i$ 行,第二个串的前 $j$ 行,转移有 $4$ 种,正好匹配,选择两个后缀使用 $if-else$,选择一个后缀使用 $if$。
朴素的 DP 是 $O(n^4)$ 的,但是我们实际上并不需要枚举最后一个的情况,只需要开 $4$ 种状态分别记录即可 $O(1)$ 转移。
注意,初始化的细节和 $if-else$ 的两个串长度不一定相同。