| rank | solved | A | B | C | D | E | F | G | H | I | J | K |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 23 | Done | O | O | O | O | O | O | Ø | O | Ø | O | Ø |
A
Solved by XLor (04:05:56, +5).
建一个 AC 自动机,然后使用 KMP 的 Fail 树进行去重。
B
Solved by XLor (04:32:57, +26).
枚举两个点,求圆心的众数。
枚举一个点,确定圆心在一条中垂线上,再枚举另外一个点,求圆心的众数。
P.S. 没有判所有直线都平行。
C
Solved by miaojie (02:38:51, +4).
答案个数是 $(\text{叶子个数}+1) \over 2$,构造答案可以将叶子按 dfs 序排序后,对半分后配对。
D
Solved by miaojie (00:05:50).
签到题。
E
Solved by ytriayggg (02:19:37, +16).
F
Solved by XLor (00:51:52).
建出矩阵后,先跑一遍横着的滑动窗口,压缩成行的最大值,再竖着跑一遍滑动窗口,得到真实最大值。
G
UpSolved by XLor.
考虑 shift-and 算法,使用 bitset 大力优化。
H
Solved by ytriayggg (04:20:13, +2).
分类讨论,若询问是最大边,使用 set 维护,否则,若使用一个数据结构维护每个点和其前驱差的最小值。
I
UpSolved by miaojie.
平面图最小割,转成对偶图求最短路。
J
Solved by ytriayggg (02:47:25).
步数是大质数,因此答案必定存在,对置换群的每个环分别考虑,原置换群每次往前走 $k$ 步。
K
UpSolved by XLor (-4).
固定点 $A$,枚举点 $B$,计算 $C$ 点到直线 $AB$ 的期望高度。
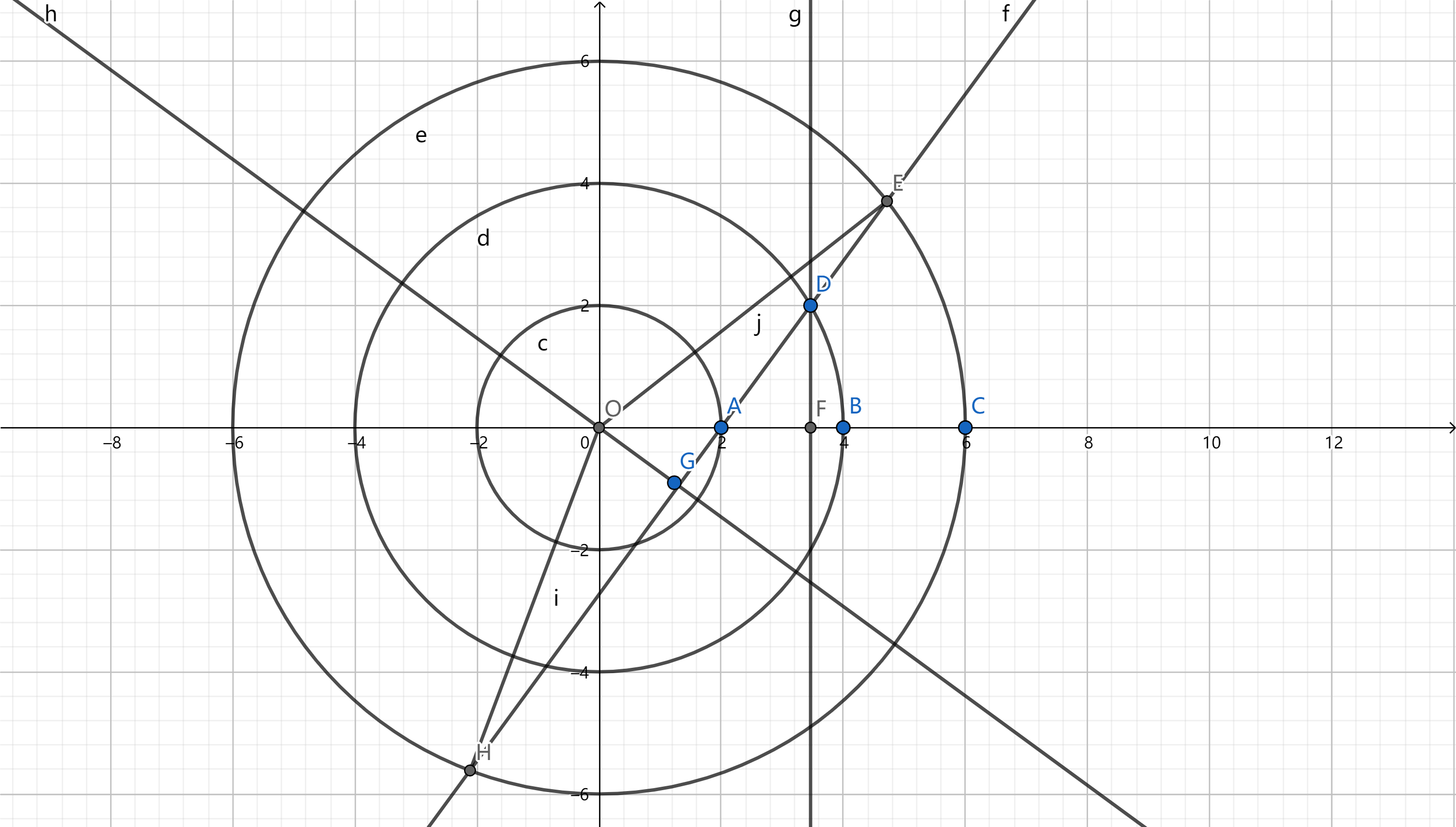
如上图,$A$ 为第一个动点,$D$ 为第二个点,通过 $\triangle ADF \sim \triangle AOG$ 可以算出线段 $OG$ 的长度,进而得到 $\angle OEH$ ($\angle OHE$)。此时,可以丢弃这个斜着的图形,只保留该角度 $\alpha$ 放正图形容易进行积分,得到期望高度为 ${4R \over 2\pi}(\alpha\sin\alpha+\cos\alpha)$。
注意,由于做了两次积分,两个随机变量都服从 $[0, 2\pi]$ 的均匀分布,需要除两次 $2\pi$。