跃迁引擎启动

最小回文划分

发表于 更新于 分类于 阅读次数：

问题

给定一个字符串 $s(1\le |s| \le 10^5)$ ，求最小的 $k$ ，使得存在 $s_1,s_2,\dots,s_k$ ，满足 $s_i(1\le i \le k)$ 均为回文串，且 $s_1,s_2, \dots ,s_k$ 依次连接后得到的字符串等于 $s$ 。

暴力做法

考虑动态规划，记 $dp[i]$ 表示 $s$ 长度为 $i$ 的前缀的最小划分数，转移只需要枚举以第 $i$ 个字符结尾的所有回文串

$$
dp[i]=1+\min_{ s[j+1..i] \text{ 为回文串} } dp[j]
$$

由于一个字符串最多会有 $O(n^2)$ 个回文子串，因此上述算法的时间复杂度为 $O(n^2)$。

引理与证明

定义

由于一个字符串最多会有 $O(n^2)$ 个回文子串，因此上述算法的时间复杂度为 $O(n^2)$ ，无法接受，为了优化转移过程，下面给出一些引理。

记字符串 $s$ 长度为 $i$ 的前缀为 $pre(s,i)$ ，长度为 $i$ 的后缀为 $suf(s,i)$ 。

周期：若 $0< p \le |s|$ ， $\forall 1 \le i \le |s|-p,s[i]=s[i+p]$ ，就称 $p$ 是 $s$ 的周期。

border：若 $0 \le r < |s|$ ， $pre(s,r)=suf(s,r)$ ，就称 $pre(s,r)$ 是 $s$ 的 border。

周期和 border 的关系

$t$ 是 $s$ 的 border，当且仅当 $|s|-|t|$ 是 $s$ 的周期。

证明：

若 $t$ 是 $s$ 的 border，那么 $pre(s,|t|)=suf(s,|t|)$ ，因此 $\forall 1\le i \le |t|, s[i]=s[|s|-|t|+i]$ ，所以 $|s|-|t|$ 就是 $s$ 的周期。

若 $|s|-|t|$ 为 $s$ 周期，则 $\forall 1 \le i \le |s|-(|s|-|t|)=|t|,s[i]=s[|s|-|t|+i]$ ，因此 $pre(s,|t|)=suf(s,|t|)$ ，所以 $t$ 是 $s$ 的 border。

引理 1

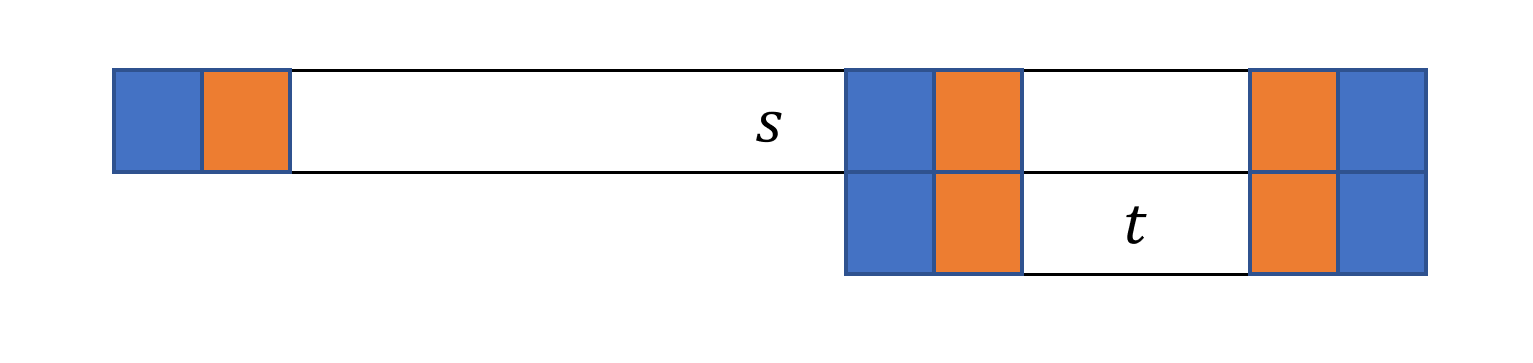
$t$ 是回文串 $s$ 的后缀， $t$ 是 $s$ 的 border 当且仅当 $t$ 是回文串。

证明：

对于 $1 \le i \le |t|$ ，由 $s$ 和 $t$ 为回文串，因此有 $s[i]=s[|s|-i+1]=s[|s|-|t|+i]$ ，所以 $t$ 是 $s$ 的 border。

对于 $1 \le i \le |t|$ ，由 $t$ 是 $s$ 的 border，有 $s[i]=s[|s|-|t|+i]$ ，由 $s$ 是回文串，有 $s[i]=s[|s|-i+1]$ ，因此 $s[|s|-i+1]=s[|s|-|t|+i]$ ，所以 $t$ 是回文串。

下图中，相同颜色的位置表示字符对应相同。

引理 2

$t$ 是回文串 $s$ 的 border ( $|s|\le 2|t|$ )， $s$ 是回文串当且仅当 $t$ 是回文串。

证明：

若 $s$ 是回文串，由引理 $1$ ， $t$ 也是回文串。

若 $t$ 是回文串，由 $t$ 是 $s$ 的 border，因此 $\forall 1 \le i \le |t|, s[i]=s[|s|-|t|+i]=s[|s|-i+1]$ ，因为 $|s| \le 2|t|$ ，所以 $s$ 也是回文串。

引理 3

$t$ 是字符串 $s$ 的 border，则 $|s|-|t|$ 是 $s$ 的周期， $|s|-|t|$ 为 $s$ 的最小周期，当且仅当 $t$ 是 $s$ 的最长回文真后缀。

引理 4

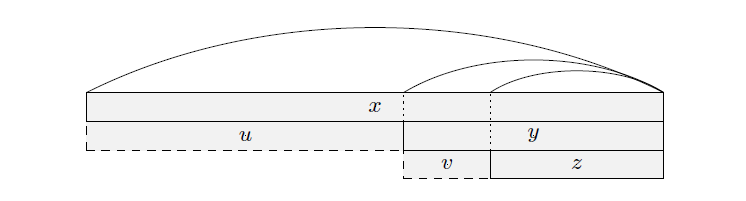
$x$ 是一个回文串，$y$ 是 $x$ 的最长回文真后缀，$z$ 是 $y$ 的最长回文真后缀。令 $u,v$ 分别为满足 $x=uy,y=vz$ 的字符串，则有下面三条性质

  1. $|u| \ge |v|$ ；

  2. 如果 $|u| > |v|$ ，那么 $|u| > |z|$ ；

  3. 如果 $|u| = |v|$ ，那么 $u=v$。

证明：

  1. 由引理 $3$ 的推论， $|u|=|x|-|y|$ 是 $x$ 的最小周期， $|v|=|y|-|z|$ 是 $y$ 的最小周期。考虑反证法，假设 $|u| < |v|$ ，因为 $y$ 是 $x$ 的后缀，所以 $u$ 既是 $x$ 的周期，也是 $y$ 的周期，而 $|v|$ 是 $y$ 的最小周期，矛盾。所以 $|u| \ge |v|$ 。

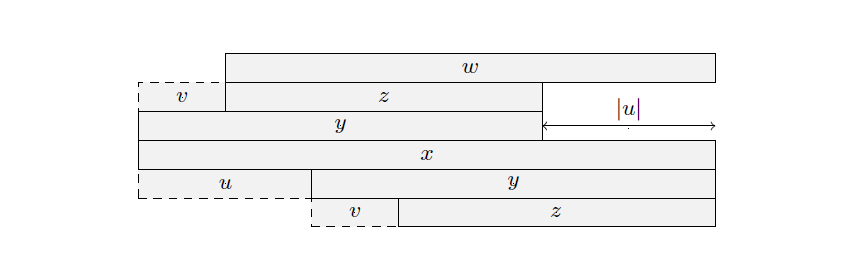
  2. 因为 $y$ 是 $x$ 的 border，所以 $v$ 是 $x$ 的前缀，设字符串 $w$ ，满足 $x=vw$ （如下图所示），其中 $z$ 是 $w$ 的 border。考虑反证法，假设 $|u| \le |z|$ ，那么 $|zu| \le 2|z|$ ，所以由引理 $2$ ， $w$ 是回文串，由引理 $1$ ， $w$ 是 $x$ 的 border，又因为 $|u| > |v|$ ，所以 $|w| > |y|$ ，矛盾。所以 $|u| > |z|$ 。

  3. $u,v$ 都是 $x$ 的前缀， $|u|=|v|$ ，所以 $u=v$ 。

推论

$s$ 的所有回文后缀按照长度排序后，可以划分成 $\log |s|$ 段等差数列。

证明：

设 $s$ 的所有回文后缀长度从小到大排序为 $l_1,l_2,\dots,l_k$ 。对于任意 $2 \le i \le k-1$ ，若 $l_{i}-l_{i-1}=l_{i+1}-l_{i}$ ，则 $l_{i-1},l_{i},l_{i+1}$ 构成一个等差数列。否则 $l_{i}-l_{i-1}\neq l_{i+1}-l_{i}$ ，由引理 $4$ ，有 $l_{i+1}-l_{i}>l_{i}-l_{i-1}$ ，且 $l_{i+1}-l_{i}>l_{i-1}$ ， $l_{i+1}>2l_{i-1}$ 。因此，若相邻两对回文后缀的长度之差发生变化，那么这个最大长度一定会相对于最小长度翻一倍。显然，长度翻倍最多只会发生 $O(\log |s|)$ 次，也就是 $s$ 的回文后缀长度可以划分成 $\log |s|$ 段等差数列。

该推论也可以通过使用弱周期引理，对 $s$ 的最长回文后缀的所有 border 按照长度 $x$ 分类， $x \in [2^0,2^1),[2^1,2^2),\dots,[2^k,n)$ ，考虑这 $\log |s|$ 组内每组的最长 border 进行证明。详细证明可以参考金策的《字符串算法选讲》和陈孙立的 2019 年 IOI 国家候选队论文《子串周期查询问题的相关算法及其应用》。

做法

有了上述结论后，我们现在可以考虑如何优化 $dp$ 的转移。

回文树上的每个节点 $u$ 需要多维护两个信息， $diff[u]$ 和 $slink[u]$ 。 $diff[u]$ 表示节点 $u$ 和 $fail[u]$ 所代表的回文串的长度差，即 $len[u]-len[fail[u]]$ 。 $slink[u]$ 表示 $u$ 一直沿着 fail 向上跳到第一个节点 $v$ ，使得 $diff[v] \neq diff[u]$ ，也就是 $u$ 所在等差数列中长度最小的那个节点。

根据上面证明的结论，如果使用 $slink$ 指针向上跳的话，每向后填加一个字符，只需要向上跳 $O(\log |s|)$ 次。因此，可以考虑将一个等差数列表示的所有回文串的 $dp$ 值之和（在原问题中指 $\min$ ），记录到最长的那一个回文串对应节点上。

$g[v]$ 表示 $v$ 所在等差数列的 $dp$ 值之和，且 $v$ 是这个等差数列中长度最长的节点，则 $g[v]=\sum_{slink[x]=v} dp[i-len[x]]$ 。

下面我们考虑如何更新 $g$ 数组和 $dp$ 数组。以下图为例，假设当前枚举到第 $i$ 个字符，回文树上对应节点为 $x$ 。 $g[x]$ 为橙色三个位置的 $dp$ 值之和（最短的回文串 $slink[x]$ 算在下一个等差数列中）。 $fail[x]$ 上一次出现位置是 $i-diff[x]$ （在 $i-diff[x]$ 处结束）， $g[fail[x]]$ 包含的 $dp$ 值是蓝色位置。因此， $g[x]$ 实际上等于 $g[fail[x]]$ 和多出来一个位置的 $dp$ 值之和，多出来的位置是 $i-(slink[x]+diff[x])$ 。最后再用 $g[x]$ 去更新 $dp[i]$ ，这部分等差数列的贡献就计算完毕了，不断跳 $slink[x]$ ，重复这个过程即可。具体实现方式可参考例题代码。

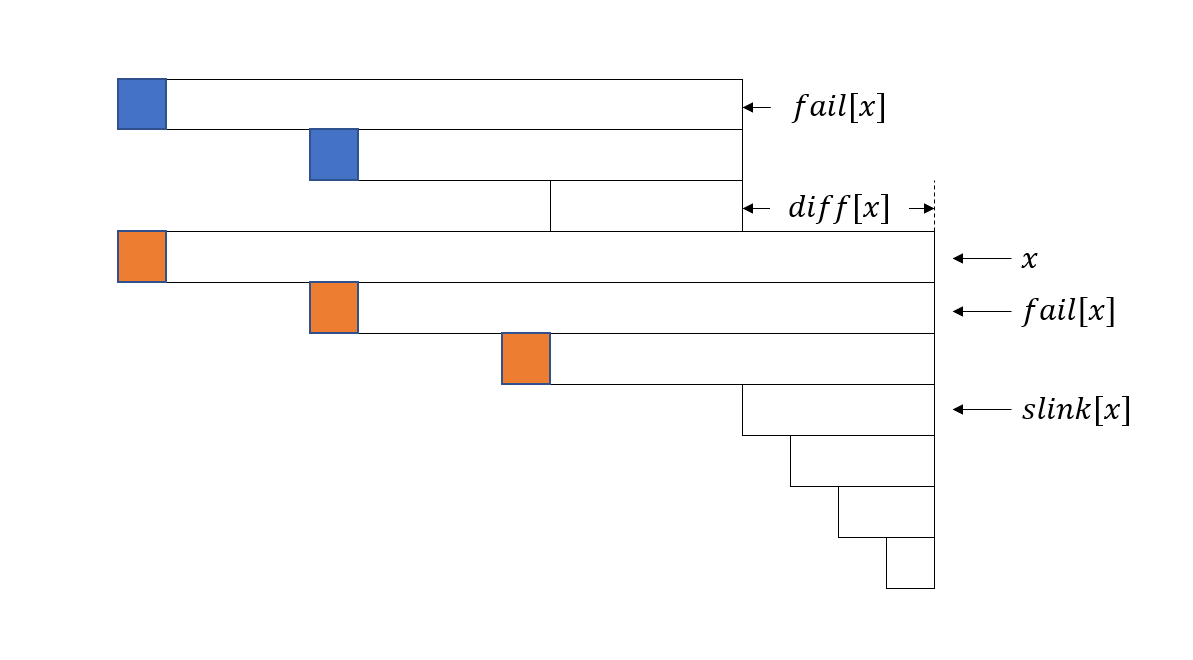
最后，上述做法的正确性依赖于：如果 $x$ 和 $fail[x]$ 属于同一个等差数列，那么 $fail[x]$ 上一次出现位置是 $i-diff[x]$ 。

证明：

根据引理 $1$ ， $fail[x]$ 是 $x$ 的 border，因此其在 $i-diff[x]$ 处出现。

假设 $fail[x]$ 在 $(i-diff[x],i)$ 中的 $j$ 位置出现。由于 $x$ 和 $fail[x]$ 属于同一个等差数列，因此 $2|fail[x]| \ge x$ 。多余的 $fail[x]$ 和 $i-diff[x]$ 处的 $fail[x]$ 有交集，记交集为 $w$ ，设串 $u$ 满足 $uw=fail[x]$ 。用类似引理 $1$ 的方式可以证明， $w$ 是回文串，而 $x$ 的前缀 $s[i-len[x]+1..j]=uwu$ 也是回文串，这与 $fail[x]$ 是 $x$ 的最长回文前缀（后缀）矛盾。

Codeforces 932G Palindrome Partition

构造字符串 $t= s[0]s[n - 1]s[1]s[n - 2]s[2]s[n - 3] \dots s[n / 2 - 1]s[n / 2]$ ，问题等价于求 $t$ 的偶回文划分方案数，把上面的转移方程改成求和形式并且只在偶数位置更新 $dp$ 数组即可。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int maxn = 1000000 + 5;

inline int add(int x, int y) {
  x += y;
  return x >= mod ? x -= mod : x;
}

namespace pam {
  int sz, tot, last;
  int ch[maxn][26], len[maxn], fail[maxn];
  int cnt[maxn], dep[maxn], dif[maxn], slink[maxn];
  char s[maxn];
  int node(int l) {
    sz++; 
    memset(ch[sz], 0, sizeof(ch[sz]));
    len[sz] = l; 
    fail[sz] = 0;
    cnt[sz] = 0;
    dep[sz] = 0;
    return sz;
  }
  void clear() {
    sz = -1; last = 0;
    s[tot = 0] = '$';
    node(0); node(-1);
    fail[0] = 1;
  }
  int getfail(int x) {
    while (s[tot - len[x] - 1] != s[tot]) x = fail[x];
    return x;
  }
  void insert(char c) {
    s[++tot] = c;
    int now = getfail(last);
    if (!ch[now][c - 'a']) {
      int x = node(len[now] + 2);
      fail[x] = ch[getfail(fail[now])][c - 'a'];
      dep[x] = dep[fail[x]] + 1;
      ch[now][c - 'a'] = x;

      dif[x] = len[x] - len[fail[x]];
      if (dif[x] == dif[fail[x]]) slink[x] = slink[fail[x]];
      else slink[x] = fail[x];
    }
    last = ch[now][c - 'a'];
    cnt[last]++;
  }
}
using pam::len;
using pam::fail;
using pam::slink;
using pam::dif;

int n, dp[maxn], g[maxn]; char s[maxn], t[maxn];

int main() {
  pam::clear();
  scanf("%s", s + 1); 
  n = strlen(s + 1);
  for (int i = 1, j = 0; i <= n; i++) t[++j] = s[i], t[++j] = s[n - i + 1];
  dp[0] = 1;
  for (int i = 1; i <= n; i++) {
    pam::insert(t[i]);
    for (int x = pam::last; x > 1; x = slink[x]) {
      g[x] = dp[i - len[slink[x]] - dif[x]];
      if (dif[x] == dif[fail[x]]) g[x] = add(g[x], g[fail[x]]);
      if (i % 2 == 0) dp[i] = add(dp[i], g[x]);
    }
  }
  printf("%d", dp[n]);
  return 0;
}

参考资料

  • 本文作者： XLor
  • 本文链接： https://xlor.cn/2019/11/mpf/
  • 版权声明： 本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！